Уроки 22 - 23
§14. Математическое моделирование
Содержание урока
Разработка математической модели
Построение компьютерной модели
Практическая работа № 10 «Полёт шарика»
Практическая работа № 11 «Полёт шарика-2»
Разработка математической модели
На этапе разработки математической модели нужно:
1) выделить исходные данные, существенные для решения данной задачи;
2) построить математическую модель, отражающую только существенные свойства оригинала.
Какие данные в формулировке задачи 2, на ваш взгляд, существенные, а какие — нет?
Введём некоторые допущения:
• мяч — материальная точка (его размеры малы в сравнении с высотой полета);
• сопротивление воздуха не учитывается.
При решении задачи могут использоваться несколько моделей разных типов. Например, для лучшею понимания полезно построить графическую модель задачи (рис. 3.1).
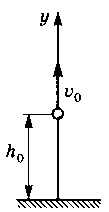
Рис. 3.1
За начало координат удобно принять точку, отсуда вылетает мяч. Обозначим через и v0 начальную скорость мяча, через h0 — начальную высоту мяча h0 = 1,5 м) — это исходные данные. Нужный результат — это время полёта мяча tn (рис. 3.2).
Рис. 3.2
Графическая модель не даёт ответа на поставленный вопрос, а только позволяет лучше понять задачу. Поэтому для численных расчётов нужно построить математическую модель — связать с помощью законов физики известные данные и результат.
Координата y при движении тела, брошенного вертикально вверх, вычисляется по формуле:
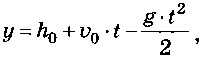
где g ≈ 9,81 м/с2 — ускорение свободного падения. Эта формула и представляет собой математическую модель задачи. В ней нет упоминания о Васе, мяче, и т. п., есть только условные обозначения. Мы выполнили формализацию — построили формальную модель на языке математических формул.
По условию задачи нужно найти время tn, при котором мяч упадёт на земную поверхность. Запишите условие «мяч упадёт на землю» в виде формулы и затем запишите уравнение, которое нужно решить.
Следующая страница  Тестирование модели
Тестирование модели

