Уроки 22 - 23
§14. Математическое моделирование

Содержание урока

Постановка задачи

Разработка математической модели

Тестирование модели

Построение компьютерной модели

Эксперимент с моделью

Анализ результатов

Выводы

Вопросы и задания

Практическая работа № 10 «Полёт шарика»

Практическая работа № 11 «Полёт шарика-2»

Построение компьютерной модели

Мы только что получили модель задачи, которая свелась к уравнению:

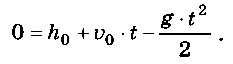
Это квадратное уравнение можно решить аналитически, получить точный ответ в виде формул. Эти формулы нужно заложить в программу. Приведём программы на алгоритмическом языке и на языке Паскаль, которые находят решение по формулам, известным вам из курса математики:

Изучите программу и ответьте на вопросы.

— Что обозначают переменные а, b, с, D, t1 и t2?
— Какое из двух решений квадратного уравнения нужно выбрать?
— Какой результат возвращает стандартная функция sqrt?
— Может ли случиться так, что уравнение не будет иметь вещественных корней?
— Как изменить начальную высоту шарика и начальную скорость?

В более сложных случаях точное решение найти не удаётся, и приходится строить компьютерную имитационную модель. Для этого можно применить табличный процессор (OpenOffice Calc, Microsoft Excel и т.п.), написать собственную программу на одном из языков программирования или использовать готовую среду для моделирования (например, Simulink или VisSim). К сожалению, такие модели чаще всего дают только приближённое (неточное) решение задачи.

Попробуем написать свою программу для имитационного моделирования. Как вы знаете, компьютер — это дискретное устройство, он работает с дискретными данными. Поэтому нужно выполнить дискретизацию задачи. Мы будем вычислять скорость и высоту шарика только в отдельные моменты времени 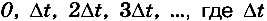— это небольшой интервал времени, который называют интервалом дискретизации. Таким образом, рассматриваются только значения времени 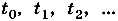, где .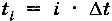

Пусть в начале отрезка [t_i, t_i+1] (при t = t_t) мы знаем координату (высоту) шарика y₁ и значение его скорости v_t. Для простоты будем считать, что в течение времени t_t ≤ t < t_i+1 скорость не изменяется, а в конце отрезка изменяется скачком. Тогда координату и скорость в конце отрезка (в момент t_i+1) можно вычислить по формулам:

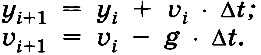
Здесь g — это ускорение свободного падения, благодаря которому изменяется скорость.

Запишите значения координаты и скорости в конце первого и второго отрезков времени (в моменты t₁ и t₂), выразив их через известные величины: .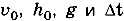

Так как в каждый конкретный момент нас интересуют только текущие значения координаты и скорости, в программе будем использовать всего одну переменную у для хранения текущей координаты (т. е. координаты в данный момент времени) и одну переменную v для хранения текущей скорости. Получается такая программа:

Изучите программу и ответьте на вопросы.

— Что обозначают переменные y, v и t?
— Какие начальные значения присваиваются переменным y, v, и t? Почему именно такие?
— Когда работа цикла завершится?
— Может ли случиться так, что цикл будет работать бесконечно?
— Что произойдёт, если в условии работы цикла использовать строгое неравенство y > 0?
— Значение какой переменной выводится в качестве результата? Почему?
— Как изменятся при уменьшении интервала дискретизации 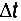длина текста программы и количество операций, выполняемых компьютером?

Для тестирования этой программы нужно провести контрольные расчёты для простых случаев с известным результатом, например для тех, которые мы ранее использовали при тестировании математической модели. Если проверка прошла удачно (противоречий не обнаружено), можно переходить к компьютерному эксперименту.

Следующая страница Эксперимент с моделью

Cкачать материалы урока