Уроки 27 - 30
Предикаты и кванторы. Логические элементы компьютера. Логические задачи
§23. Предикаты и кванторы. §24. Логические элементы компьютера. §25. Логические задачи
Содержание урока
§23. Предикаты и кванторы
§24. Логические элементы компьютера
§25. Логические задачи
Табличный метод. Задача 2
Использование алгебры логики. Задачи 5 - 6
§25. Логические задачи
Табличный метод
Задача 2
Задача 2. Перед началом турнира по шахматам болельщики высказали следующие предположения по поводу результатов:
A) Максим победит, Борис будет вторым;
Б) Борис займёт третье место, а Коля — первое;
B) Максим будет последним, а Дима — первым.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. Как распределились призовые места, если каждое место занял ровно один участник?
Запишем высказывания трёх болельщиков в форме таблицы (заголовок строки обозначает место в турнирной таблице):
Начнём «раскручивать» эту таблицу с той строчки, где больше всего информации, в данном случае — с первой. Предположим, что Максим действительно занял первое место, как и сказал болельщик «А». В этом случае «В» ошибся, поставив на первое место Диму. Тогда получается, что второй прогноз болельщика «В» верен, и Максим — последний.
Так как мы предполагали, что Максим занял первое место, получается противоречие. Следовательно, первый прогноз «А» не сбылся. Но тогда должен быть верен его второй прогноз, и Борис занял второе место. При этом он не мог занять ещё и третье место, поэтому первый прогноз болельщика «Б» неверный, а верен его второй прогноз: Коля — первый.
В этом случае Дима не может быть первым, поэтому верен первый прогноз «В»: Максим — последний. Диме осталось единственное свободное третье место.
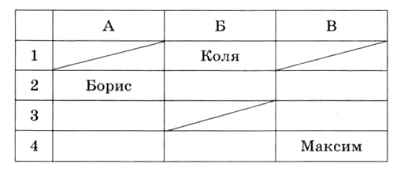
В результате места распределились так: I — Коля, II — Борис, III — Дима и IV — Максим.
Следующая страница 
Табличный метод. Задача 3
Cкачать материалы урока
