Уроки 27 - 30
Предикаты и кванторы. Логические элементы компьютера. Логические задачи
§23. Предикаты и кванторы. §24. Логические элементы компьютера. §25. Логические задачи
Содержание урока
§23. Предикаты и кванторы
§24. Логические элементы компьютера
§25. Логические задачи
Табличный метод. Задача 3
Использование алгебры логики. Задачи 5 - 6
§25. Логические задачи
Табличный метод
Задача 3
Задача 3. На одной улице стоят в ряд четыре дома, в каждом из них живёт по одному человеку. Их зовут Василий, Семён, Геннадий и Иван. Известно, что все они имеют разные профессии: скрипач, столяр, охотник и врач. Известно, что:
(1) Столяр живёт правее охотника.
(2) Врач живёт левее охотника.
(3) Скрипач живёт с краю.
(4) Скрипач живёт рядом с врачом.
(5) Семён не скрипач и не живёт рядом со скрипачом.
(6) Иван живёт рядом с охотником.
(7) Василий живёт правее врача.
(8) Василий живёт через дом от Ивана.
Определите, кто где живёт.
Из условий (1) и (2) следует, что охотник живет не с краю, потому что справа от него живёт столяр, а слева — врач. Скрипач по условию (3) живёт с краю, он может жить как слева, так и справа от остальных:

Согласно условию (4), скрипач живет рядом с врачом, поэтому он занимает крайний дом слева:

Профессии жильцов определили, остаётся разобраться с именами. Из условия (5) «Семён не скрипач и не живет рядом со скрипачом» следует, что Семён — охотник или столяр:

Из условия (6) «Иван живёт рядом с охотником» следует, что он — врач или столяр:
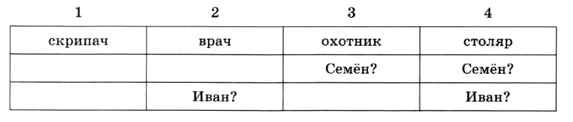
Из условия (7) «Василий живет правее врача» определяем, что Василий — охотник или столяр:

Согласно условию (8), «Василий живёт через дом от Ивана», поэтому Иван — врач, а Василий — столяр:

Тогда сразу получается, что Семён — охотник, а Геннадий должен занять оставшееся свободное место, он — скрипач:

Следующая страница  Табличный метод. Задача 4
Табличный метод. Задача 4

