Уроки 27 - 30
Предикаты и кванторы. Логические элементы компьютера. Логические задачи
§23. Предикаты и кванторы. §24. Логические элементы компьютера. §25. Логические задачи
Содержание урока
§23. Предикаты и кванторы
§24. Логические элементы компьютера
§25. Логические задачи
Табличный метод. Задача 4
Использование алгебры логики. Задачи 5 - 6
§25. Логические задачи
Табличный метод
Задача 4
Задача 4. Шесть приятелей, Саша, Петя, Витя, Дима, Миша и Кирилл, встретившись через 10 лет после окончания школы, выяснили, что двое из них живут в Москве, двое — в
Санкт-Петербурге, а двое — в Перми. Известно, что:
(1) Витя ездит в гости к родственникам в Москву и Санкт-Петербург.
(2) Петя старше Саши.
(3) Дима и Миша летом были в Перми в командировке.
(4) Кирилл и Саша закончили университет в Санкт-Петербурге и уехали в другие города.
(5) Самый молодой из них живёт в Москве.
(6) Кирилл редко приезжает в Москву.
(7) Витя и Дима часто бывают в Санкт-Петербурге по работе.
Определите, кто где живёт.
Составим таблицу, где каждая строка соответствует городу, а столбец — человеку:
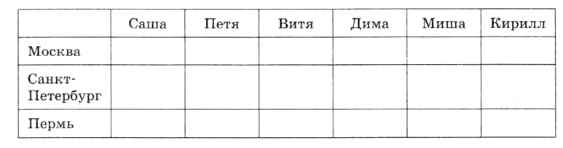
Единица в таблице будет обозначать, что человек живёт в данном городе, а ноль — что не живёт. По условию в каждом городе живут ровно 2 человека, каждый живёт только в одном городе. Поэтому в каждой строке должно быть две единицы, а в каждом столбце — одна.
Из условия (1) следует, что Витя живёт в Перми:
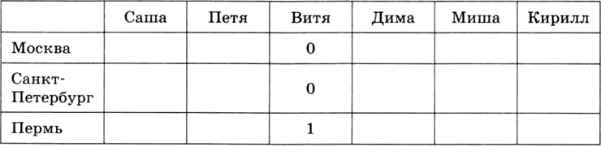
Из (2) и (5) находим, что Петя живёт не в Москве. Кроме того, как следует из (6), Кирилл — тоже не москвич.
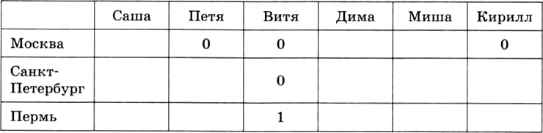
Согласно (3), Дима и Миша живут не в Перми:
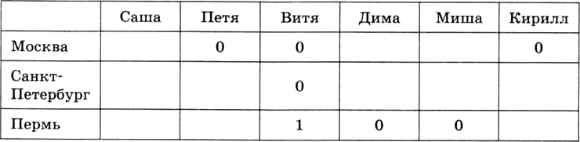
Из условия (4) делаем вывод, что Кирилл и Саша живут не в Санкт-Петербурге, отсюда сразу следует, что Кирилл живёт в Перми. Двух пермяков мы уже определили, поэтому Саша и Петя живут не в Перми:
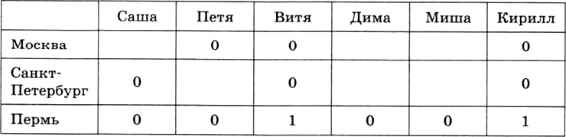
Далее определяем из таблицы, что Саша — москвич, а Петя живёт в Санкт-Петербурге:
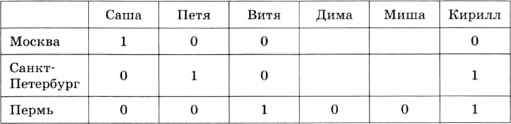
По условию (7), Витя и Дима — не петербуржцы, поэтому в Петербурге живёт Миша. Тогда Дима живёт в Москве:
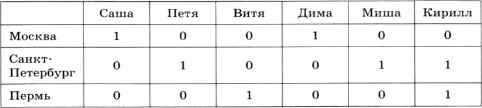
Таким образом, Саша и Дима живут в Москве, Петя и Миша — в Санкт-Петербурге, а Витя и Кирилл — в Перми.
Следующая страница 
Использование алгебры логики. Задачи 5 - 6
Cкачать материалы урока
